I made a post a while back on a video I recorded on Euler’s Identity, in which I explored the poetic elegance of mathematics. In a similar vein, a recent video I published on Tsiolkovsky’s Equation explains how, based on a few fundamental physical observations, we can represent the seemingly complex way a rocket works in one stunning, and relatively straightforward, equation.
But what exactly is Tsiolkovsky’s Equation, and how can we use it to travel to the cosmos? Well buckle up, because it’s going to be a fun ride!

To start, we need to ask a fundamental question to drive the research process. How about, “how does our rocket accelerate upwards?” Great — now we have a place to start. But what is acceleration? We’re all familiar with this word (e.g. my car is accelerating around the curve), but what does it actually mean? Acceleration essentially says how fast an object (you, me, my cat, an apple) changes its velocity, which is a vector quantity that describes the speed and direction an object is traveling, such as 60 miles per hour northward. Velocity is also a measure of the change in an object’s position over a set period of time. (If you’re more mathematically inclined, then velocity is the first derivative (meaning the rate of change) of the position function of an object with respect to time — hence miles per hour, or mi / hr. Acceleration is therefore the second derivative of position and the first derivative of velocity — I could step on the gas and increase my speed by 10 miles per hour every hour, or 10 mi/hr2). Now that we understand what it means to accelerate, we can return to our question: how does our rocket accelerate upwards?

Newton’s Second Law — ΣF = ma — helps greatly. It states that the sum (Σ is the Greek letter sigma, meaning “sum of”) of all forces F yields the product of mass and acceleration, and therefore acceleration is the net force on a given object divided by its mass. Now we need to analyze the rocket in terms of the forces acting on it. By Newton’s Third Law, we know that every force has an equal (in magnitude) but opposite (in direction) force; thus, when the exhaust particles leave the rocket’s nozzle and exert a force downward, the rocket will feel an equal but opposite force upward known as thrust (T). Since we live on Earth, we also know that gravity exerts a constant force (the actual value varies depending on altitude and density, but let’s assume Earth is a perfect sphere) of magnitude mg, where m is the object’s mass and g is the acceleration due to gravity, which is about 9.8 m/s2 (you can calculate more precise values using Newton’s Law of Gravitation). Thus, our net force on the rocket is T – mg = ma = ΣF. If the magnitude of thrust is greater than that exerted by gravity, then T – mg > 0, and therefore ΣF > 0, and thus a > 0, and the rocket shoots skyward!

Now that we know how our rocket accelerates, we can ask how it travels from one location to the next, and thus how we can predict it will travel. Remember when I said that by Newton’s Third Law, every force will have an equal but opposite reaction force? If we consider our rocket, as outlined in the above image, deep out in the space as our isolated system, then all forces are internal to the system, meaning that there is nothing outside of the rocket causing it to accelerate — it is solely the force generated by the exiting particles of exhaust fuel. Since all forces are internal to the system, the net external force exerted on the rocket is 0. This fundamental physics property is known as Conservation of Momentum, where momentum is defined as the product of an object’s mass and its velocity. A great physical demonstration of this property is a cannon.
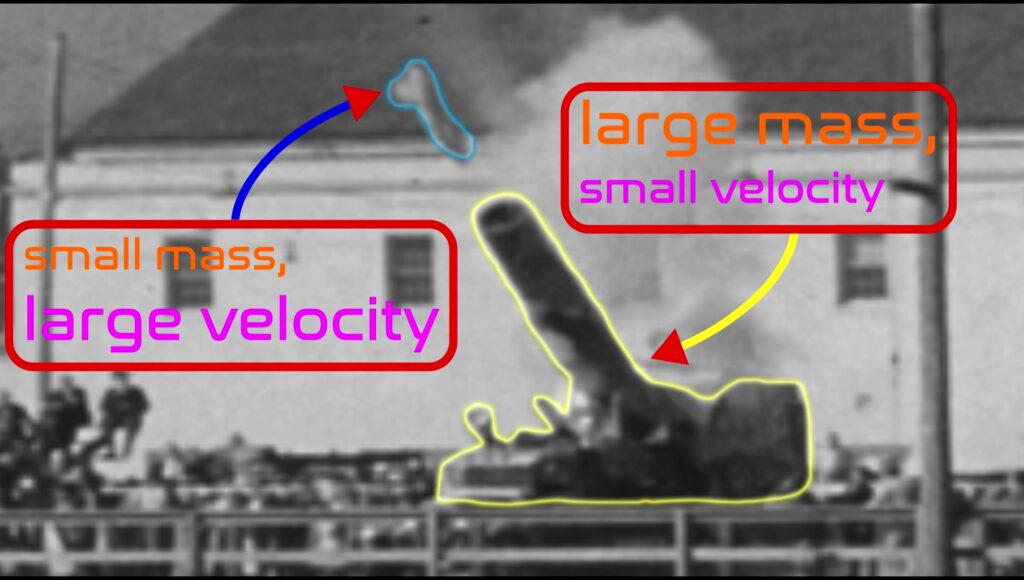
When a cannon fires its cannon ball, the projectile is shot outward at a high velocity while the cannon itself recoils with a very small velocity. Since the force from the gunpowder came from inside the cannon, all forces are internal to the system and, thus, in order for the net force of the cannon system to remain 0, the cannon must also experience an equal but opposite force to what the projectile experienced. Since we know all forces are conserved, we know that momentum (denoted by the letter p) at time 1 is equivalent to that at time 2. Hooray! We have shown that momentum is conserved! We can’t celebrate fully, though; we now need to apply what we’ve learned to the rocket itself! 🙂
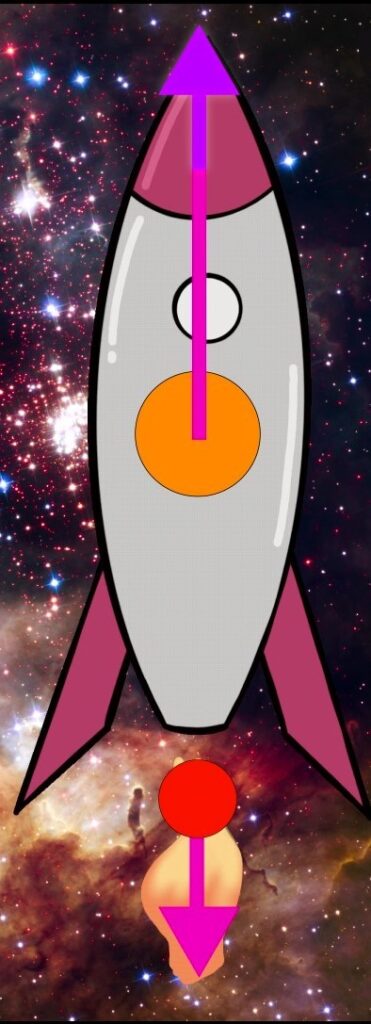
Close your eyes and imagine you’re floating through the vastness of space. Now pretend that you and your fellow astronauts decide to check the paint job on your rocket, but none of you is quite enthused. Let’s pretend you draw the short straw — er decide to volunteer — and you are watching the spacecraft as an outside observer. To your startling dismay, you see your “friends” onboard the rocket wave at you as they fire up the engines and leave you stranded behind (maybe eating the secret stash of cookies wasn’t the brightest idea after all…). Let’s ignore your severe existential crisis and enormity of self-doubt for the moment to simplify our problem. As the rocket ejects particles of fuel at some downward exhaust velocity ve after some time Δt, the mass inside the rocket decreases; you in turn see the rocket’s velocity increase by +Δv. Relative to you, the velocity of the exhaust is actually the velocity of the rocket (V + Δv) minus the exhaust velocity of the particles relative to the rocket (ve) because the exhaust is moving with the rocket. Thus, even though the particles are ejected downward, they appear to move upwards from you (on the plus side, you’ll have so much more time to contemplate the state of the universe without those noisy, good-for-nothing so-called “friends” of yours on the rocket). Notwithstanding your anxiety, you will have a moment of happiness because you will realize that momentum is being conserved, as the exhaust particles are ejected from within the rocket without any kind of net external force, as with the cannon example.
In all seriousness, momentum conservation (relative to the observer) is the veritable answer to our problem of explaining the successful functioning of the rocket: we can write an equation to express the zero net change in momentum of the rocket-exhaust system, making sure to account for the vector nature of momentum (direction matters, but which is positive — up or down, left or right — does not matter as long as we stick to one).
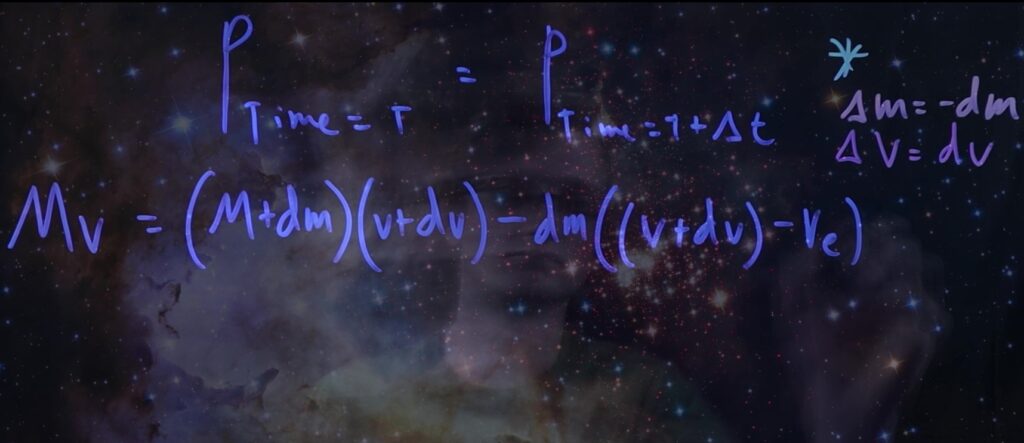
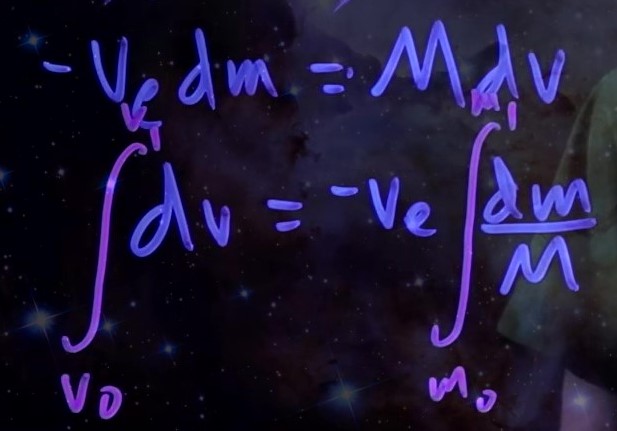
We can then simplify this initial expression by expanding (aka “foiling”) the polynomials. We arrive at a differential equation that we can integrate to remove the differentials, with our initial velocity represented as v0 and our final velocity represented as v1, and our initial mass represented as m0 and our final mass represented as m1. Note: by “final” I do not mean to imply that the rocket has burned all of its fuel; rather, I mean the velocity or mass respectively after our time interval +Δt.
Thus, after some algebra, some calculus, and a little elbow grease, we arrive at long last at Tsiolkovsky’s Equation!
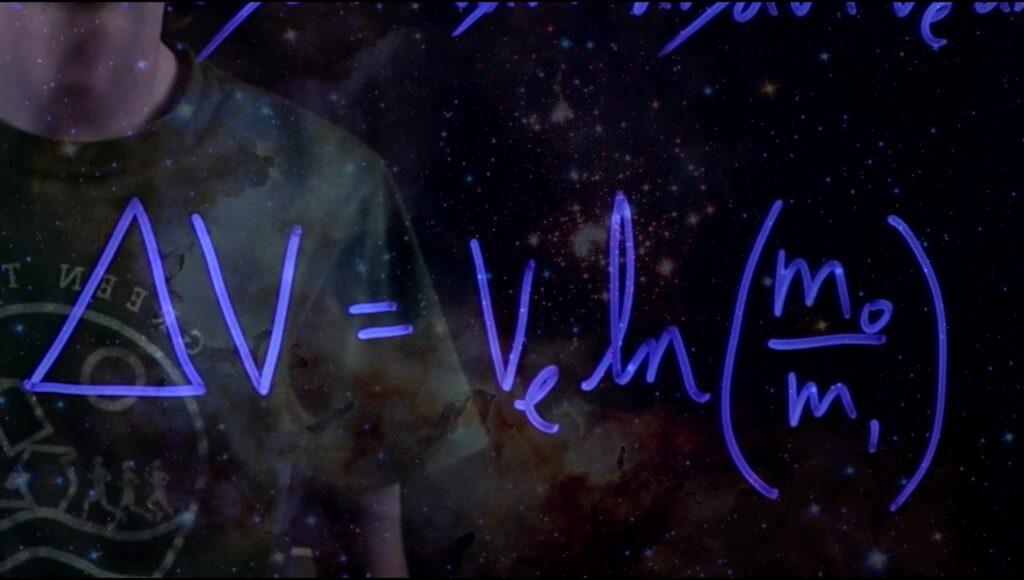
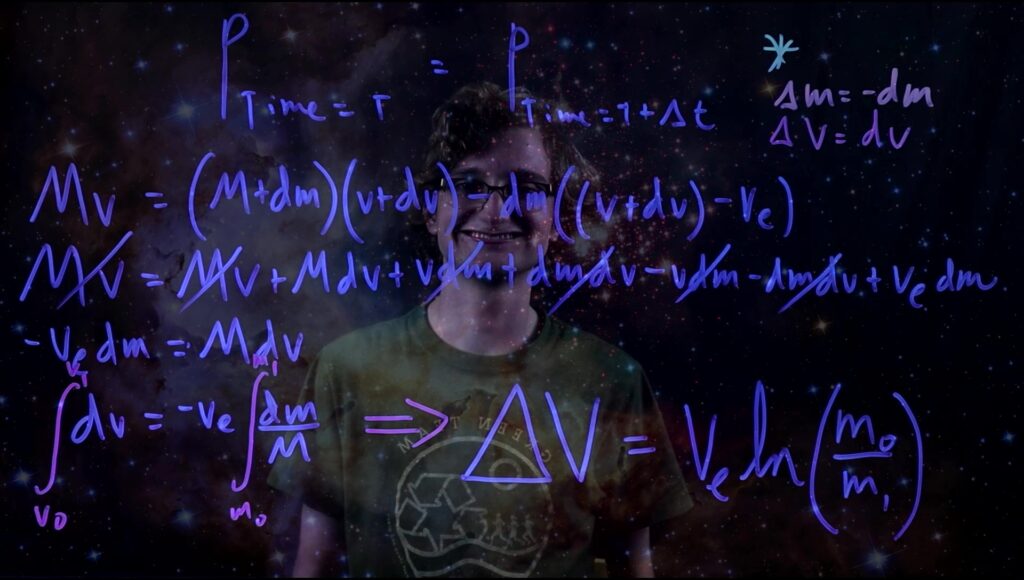
Alright — now that we have determined a mathematical model analyzing the motion of our rocket, what is it really telling us
This equation yields ΔV, or change in velocity, given a set speed ve of the exhaust particles — defined as g0Isp, where g0 is the standard acceleration due to gravity (only a conversion factor here, not the location-dependent value of gravity), and Isp is the specific impulse of the engine (the thrust of the engine through a time interval divided by the weight mg0 of the rocket) — and a starting mass of the rocket m0 and an ending mass of the rocket m1 without fuel. But what is ΔV?
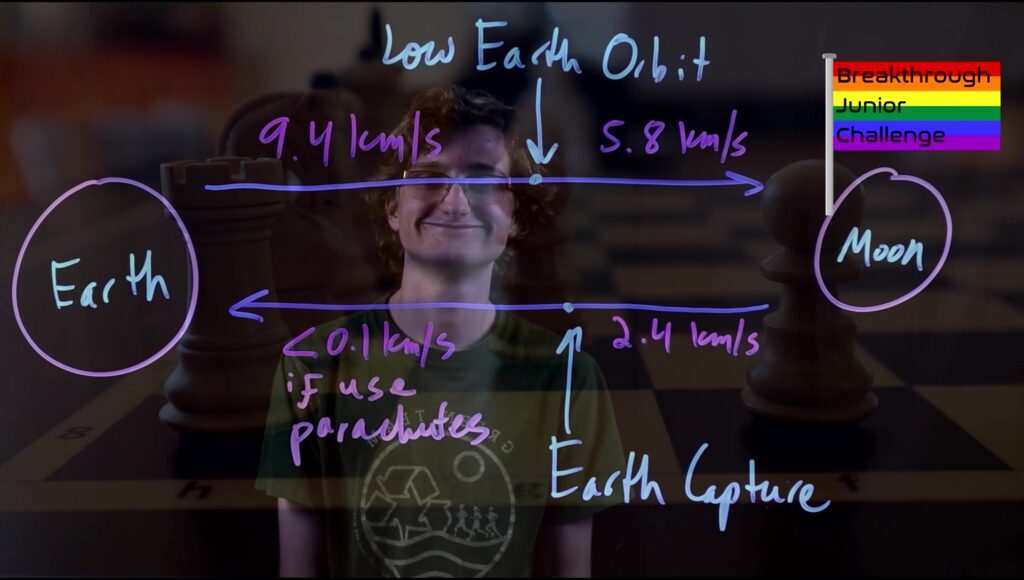
ΔV, literally, is the difference in the velocity of the rocket from after firing the engines to before firing the engines. Imagine that the universe is a cosmic board game, and our rocket is a game piece. If, say, we wanted to move our rocket from the Earth to the Moon, then we would need to add up the ΔV requirements along our given trajectory to arrive at the minimum value needed to arrive there. Gravity is an interesting player here — at first when we are trying to leave Earth, the force of gravity (as shown earlier) works against our rocket, pulling it down. Thus, we can add a -gtbo term to the end of Tsiolkovsky’s Equation to account for the affect of the acceleration due to gravity on the velocity of the rocket while the rocket is burning fuel. (The value of g will actually decrease by the inverse square relation as we move away from Earth’s surface.) Also, aerodynamic forces, such as drag, can slow our rocket down (which is why rockets have very sleek designs to minimize exposed surface area to oncoming air particles). Unsurprisingly, more testing of specific rocket designs will yield more accurate results; Tsiolkovsky’s Equation is, thus, the basis for those models.
Pat yourself on the back (because no one can hear you clap in space) because we have done it! We have solved the question that we set out to answer, and now we know how a rocket works! But is that all?
The beauty of Tsiolkovsky’s Equation lies not only in its stunning simplicity, but in its function as the key to the cosmos. However, tyranny paradoxically springs from that beauty; if that equation defines how a rocket works, it thus dictates how it must work, meaning we cannot achieve through technology beyond the limits of Tsiolkovsky’s Equation. This tyranny is rooted in a term called propellant mass fraction, or PMF for short. As its name suggests, PMF is simply the mass of the propellant divided by the total mass of the rocket. Using Tsiolkovsky’s Equation, we can quantify how much fuel is needed given a set ΔV value and starting/ending mass.
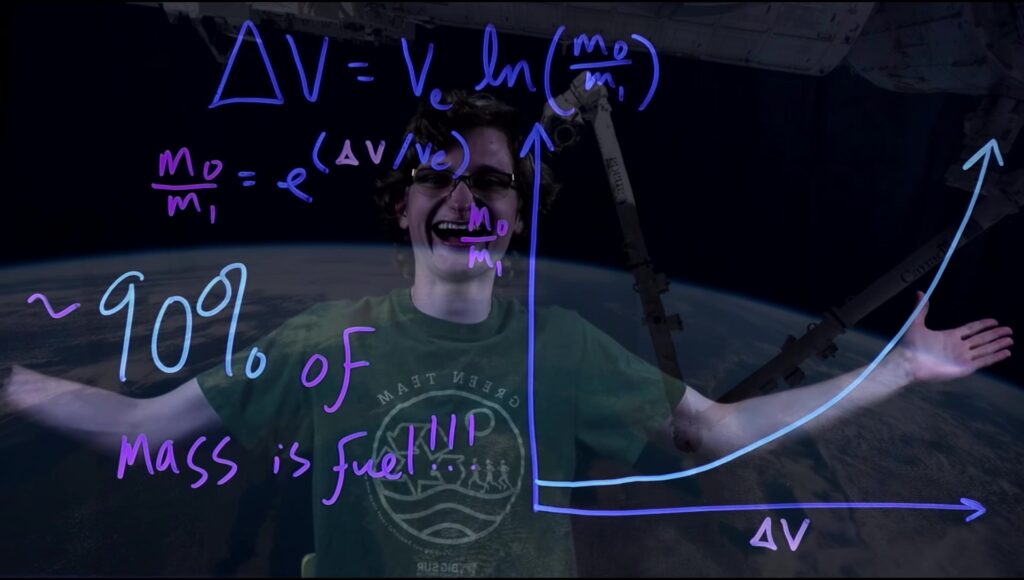
As astronaut and rocket engineer Don Pettit explains in his article on “The Tyranny of the Rocket Equation,” Tsiolkovsky’s Equation confines us to play by a limited set of rules; given particular engine, fuel, and mass constraints, we are very limited to where we can go. Furthermore, the average PMF for rockets is somewhere around 0.9 — meaning that about 90% of the rocket, by mass, is fuel. A typical car, contrast, is only 0.04 or 4%! As Pettit wryly puts it, “sitting on top of a rocket is more dangerous than sitting on a bottle of gasoline!”

I, however, see a powerful message manifested in the mathematics of spaceflight. Many people may declaim “changing the world” as a task too onerous and ambitious for any single individual to surmount; to them I say, you have the power to make a difference — you have the power to change a person’s life, and, therefore, you have the power to change the world. So starting with one small step, you can achieve a giant leap forward notwithstanding others’ unfounded doubting. You need only to believe in yourself and in science to solve any problem that plagues you, your family, your community, your nation, or the world. That, to me, is the greatest aspect of science — that we know enough to know just how little we know, but that we can take what we do know and expand from there, oftentimes reshaping even the most basic assumptions about the universe we call home. Nevertheless, that progress will not occur without people willing to break through dogmatic tyranny to challenge and further our knowledge. As such, Tsiolkovsky’s Equation reaches beyond modeling the functioning of a rocket; it is the key to an even greater challenge that embodies the indefatigable resilience of the human spirit.

As I wrote in my poem “Stardust: Launch,” seeing the SpaceX Demo-2 launch on May 30 was absolutely inspiring to me. I knew in that moment that I wanted to explain the science behind how a rocket actually works — to share my fascination, enthusiasm, and love for the process of science with the world. Furthermore, at a time when hatred divides our world, I believe we need to come together — and I believe that spaceflight is an endeavor that will bring out that solidarity in the human race and remind us of who we really are and how much we have — and have not — changed since we last had stars in our sights as a nation and a world.
Building off of the momentum of SpaceX’s recent launch (pun intended), I decided to enter the Breakthrough Junior Challenge — an annual competition open to enterprising scientists of age 13-18, in which the entrant has three minutes to explain a concept or theory in physics, life sciences, mathematics, or COVID-19 (new for 2020). The winning prize is a $250,000 scholarship for college, a $50,000 check to a nominated STEM teacher, and a $100,000 Breakthrough Lab for the winner’s school, plus an awards ceremony with scientists like Sal Khan and Bill Nye — as if I wasn’t already inspired enough!!
My video is on Tsiolkovsky’s Equation, which falls under physics (which is really just applied math). The above discussion on deriving the equation was adapted from my video; please watch it below and share it if you like!
This video is the culmination of countless hours of writing, scripting, filming, and editing; even though there was frustration at times, as with any worthwhile undertaking, the fun I had outshines it a thousand times over. Since I officially uploaded my video about a week ago, my joy has only increased exponentially — the community reaction has been overwhelmingly positive! It’s so refreshing to see kids from every creed, color, and country come together in an atmosphere of kindness and support to share and discuss really big ideas about science and the way the world works. Just days ago, I was cracking corny Quantum Physics jokes pertaining to the Heisenberg Uncertainty Principle (see image) with Mahdi, a competitor in Morocco. I was professing my love for the physicist Richard Feynman in a conversation about nanoparticles with Zuairia, a competitor from India. I was discussing the fractal Mandelbrot Set and the Feigenbaum Constant with Yunhui, a competitor from Korea.
But what I took away did not solely pertain to physics, or mathematics, or chemistry, or biology — I saw diverse people coming together with open arms online while in the midst of coronavirus. I saw so much support and discourse between people all over the world. I saw raw hope.
In my mind, that’s what the Breakthrough Junior Challenge is all about. The money is absolutely unbelievable, but that’s really not the point. The point is to break through these invisible and nonexistent barriers we construct that separate us from them — for from knowledge comes understanding, from understanding comes appreciation, and from appreciation comes love. A love that is pure and unconditional. A love that is of humanity, by humanity, and for humanity. A love that unites us as one — as one human family against discrimination, racism, and war.
If you are reading these words, then (virtual) high five! Know that someone cares about you. Even if you feel as if you are alone and floating out there in the universe (which we all are right now, just on planet Earth), you are never truly alone. Until next time, have a mathtastic day!

Note: The amazing cartoons throughout this post and my video — such as the above spaceman — were created by my awesome friend Seth Knoop. Seth, this project would not have been what it is without your gracious assistance. Thank you!!
